Quantify Extracted Signal

Jump to step-by-step instructions in DigitalMicrograph 3

Probability of inelastic scattering

The probability \(P_{k}\) that a given incident beam electron will end up as a count in the core-edge \(k\) of a particular element is directly proportional to the projected (areal) density, \(N\), of atoms of that element.

\(P{_{k}}=N\sigma _{k}\)

The constant of proportionality, \(\sigma _{k}\), is a factor that depends on the experimental conditions and on the limits over which you integrate the edge counts. It reflects the intrinsic scattering strength of shell \(k\) of the element.

\(P_{k}=\frac{I_{k}}{I_{t}}\)

The probability \(P_{k}\) can also be measured from the energy loss spectrum of interest by taking the extracted edge count integral \(I_{k}\) and dividing by the total number of counts in the spectrum.

Hence, you can equate the two yielding the areal density of atoms present in terms of measurable quantities:

\(N = I_{k}/\sigma _{k}I_{t}\)

Effect of plural scattering on core-loss edges

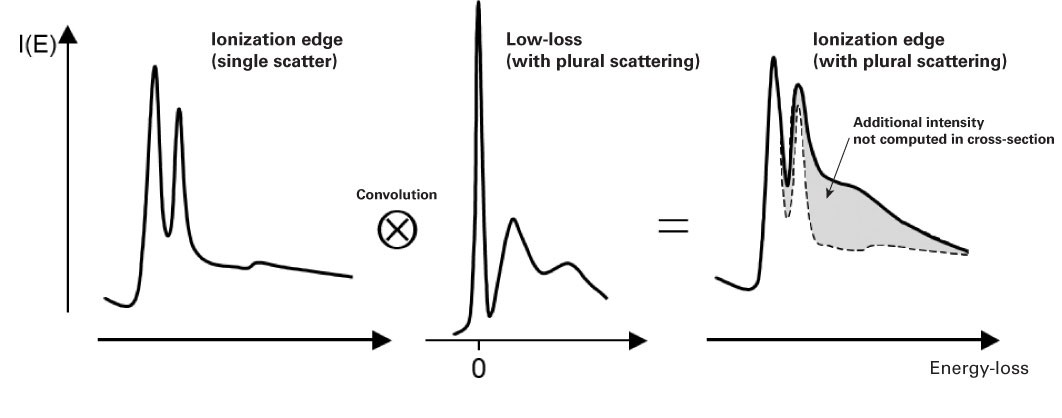
While quantification is simpler without plural scattering, it may occur, and it is important to know how plural scattering can impact your quantification. Specifically, it can:

• Redistribute the core-loss intensity – Due to a convolution of the edge shape and low-loss spectrum

• Alter the edge shape and intensity

  • Invalidates the computed cross-section

  • Reduces the signal-to-background ratio (SBR) when it shifts the edge intensity to higher losses and increases the preceding background

• In general, higher Z and thicker samples are more affected by plural scattering

Plural scattering considerations

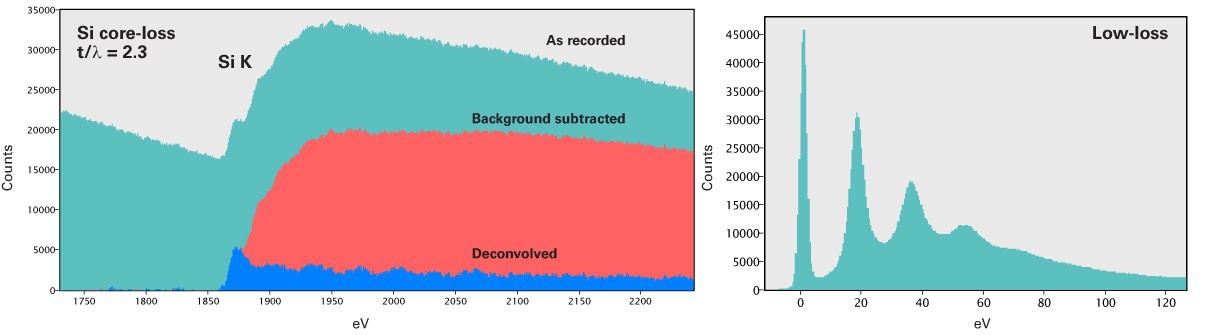
It is useful to know the impact that plural scattering may have on your quantification. Samples have a finite thickness and you need to decide if the local thickness is low enough to assume plural scattering is negligible (e.g., \(t/\lambda =0.3\), plural scattering contribution is approximately 15%).

While most quantification equations assume no plural scattering, you can remove it using deconvolution (Fourier-based methods) or incorporate it into the quantification. Here are guidelines for the types of quantification routines you can use based on the level of plural scattering present in your sample.

Measurement type	\(t/\lambda\)
Linear least squares (LLS) fitting (<1500 eV)	0.0 – 1.0
LLS fitting (>1500 eV)	0.0 – 2.0
LLS with deconvolution	0.3 – 2.0
Thickness measurements	0.15 – 6.0

Absolute quantification without plural scattering

When you safely ignore plural scattering, the areal density of atoms (atoms/nm²) of type, \(k\), can be approximated by:

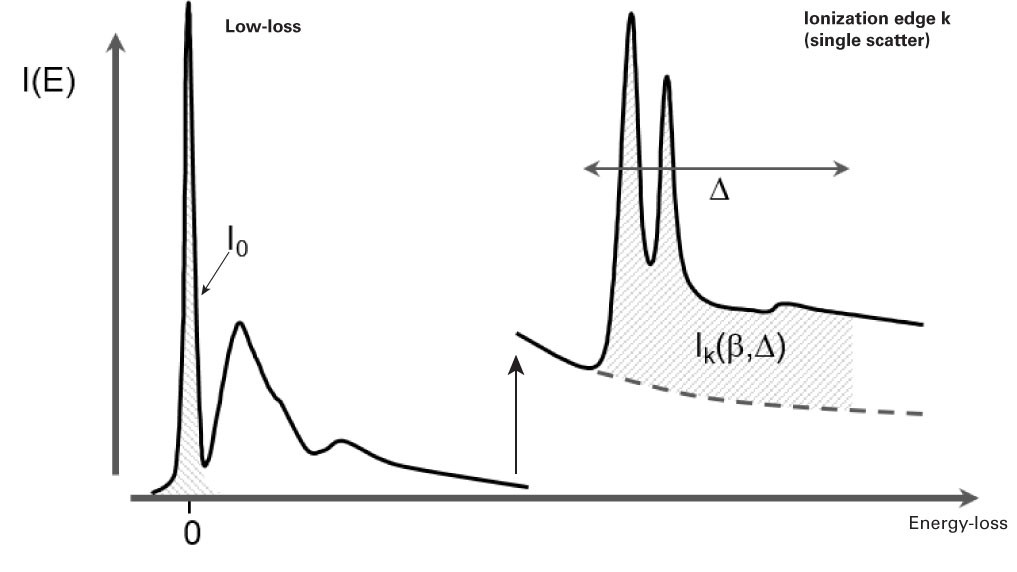
\(N = \frac{I_{k}^{1} (\beta , \Delta )}{I_{o}(\beta ) \sigma _{k} (\beta , \Delta )}\)

where

• \(I_{k}^{1} (\beta , \Delta )\) = Integral edge \(k\) with no plural scattering integrated over a window \(\Delta\)

• \(I_{0}\) = Zero-loss integral

• \(\beta\) = Effective collection angle

• \(\Delta\) = Signal integration width

• \(\sigma _{k}\left ( \beta ,\Delta \right )\) = Partial inelastic scattering cross-section

Absolute quantification with plural scattering

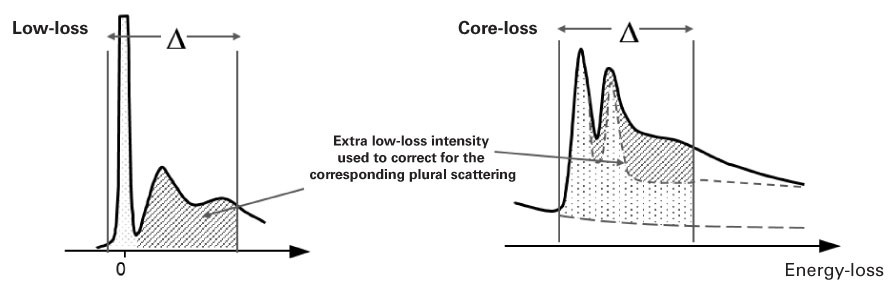
When you do not remove plural scattering, you can apply an approximate correction:

\(N\approx \frac{I_{k}(\beta ,\Delta )}{I_{low}(\beta ,\Delta )\sigma _{k}(\beta ,\Delta )}\)

where

• \(I_{low}( \beta,\Delta)\) = Low-loss intensity integrated up to energy loss \(\Delta\)

When you divide by \(I_{low}( \beta,\Delta)\) instead of \(I_{0}\), this approximately compensates for an extra signal from plural scattering. If the low-loss signal is available (in the same spectrum or a DualEELS™ pair), DigitalMicrograph^® EELS analysis will automatically include this correction.

Remove plural scattering

Plural scattering is a collection of independent events and follows predictable statistics. We can exploit this to deconvolve the effect of plural scattering from the spectrum and recover the single scattering distribution. The removal of plural scattering will improve background fit and cross­-section agreement, but not the signal­-to­-noise ­ratio (SNR) for microanalysis.

Fourier-log deconvolution

Starting with Poisson statistics for the scattering events, it can be shown that the single scattering distribution \(j^{1}\left ( E \right )\) can be derived from the recorded spectrum \(j\left ( E \right )\) using:

\(j^{1}\left ( \nu \right )=g\left ( \nu \right )ln\left [ \frac{j\left ( \nu \right )}{z\left ( \nu \right )} \right ]\)

where

• \(\nu\) = Fourier-frequency

• \(g(\nu)\) = Reconvolution function to remove noise amplification (e.g., Fourier transform (FT) of ZLP or a Gaussian of the same full width at half maximum (FWHM))

• \(z(\nu)\) = FT of the ZLP

The inverse FT of \(j^{1}(v)\) will give the signal scattering distribution. This formula needs a spectrum from zero-loss up to edge of interest, and is therefore not suitable for higher energy edges. However, it is ideal for low-loss analysis such as plasmon fingerprinting and dielectric function analysis.

Fourier-ratio deconvolution

For an isolated core-loss edge, we can treat the low-loss spectrum as an instrument broadening function and employ classical deconvolution techniques. The single scattering distribution \(j_{k}^{1}(E)\) is derived from the core-loss spectrum \(j_{k}(E)\) and corresponding low-loss spectrum \(j_{low}(E)\) using:

\(j_{k}^{1}(\nu )=\frac{g(\nu )j_{k}(\nu )}{j_{low}(\nu )}\)

where

• \(\nu\) = Fourier-frequency

• \(g(\nu )\) = Reconvolution function (e.g., FT of ZLP/Gaussian)

This formula is useful for high-loss edges (but requires corresponding low-loss spectrum). When you use this formula, you must remove the leading edge background prior to deconvolution for the Fourier analysis to be valid.

Relative quantification

It may not always be possible (or desirable) to acquire the low-loss distribution along with every core-loss spectrum. In this case, relative quantification is still possible.

You can obtain an atomic ratio of species \(A\) and \(B\) following the formula below where the zero-loss integral \(I_{0}\) divides out of the equation:

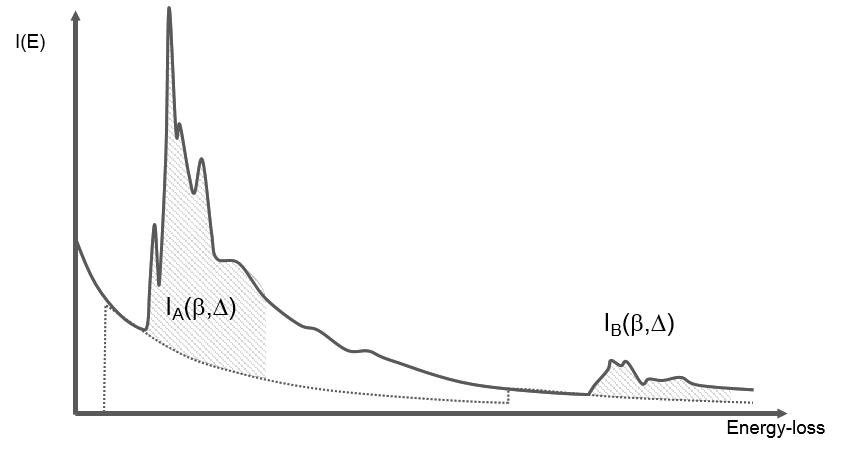
\(\frac{N_{A}}{N_{B}}=\frac{conc. A}{conc. B}\approx \frac{I_{A}(\beta ,\Delta )\sigma _{B}(\beta ,\Delta )}{I_{B}(\beta ,\Delta )\sigma_{A}(\beta ,\Delta )}\)

Where possible, use the same edge type to cancel computed cross-sections errors. Likewise, the use of the same signal windows widths will partially correct for plural scattering if \(A\) and \(B\) are edges of similar shape. This also corrects for some artifacts, including thickness and diffraction contrast.

Determine the partial cross-section \(\sigma(\beta ,\Delta )\)

You can describe inelastic scattering process by:

\(\frac{d^{2}\sigma }{d\Omega dE}=\frac{8a_{0}^{2}R^{2}}{Em_{0}\nu ^{2}}\left ( \frac{1}{\theta ^{2}+\theta_{E} ^{2}} \right )\frac{df_{n}}{dE}\)

where

• \(\Omega\) = Solid angle of scattering

• \(E\) = Energy loss

• \(R\) = Rydberg energy (13.6 eV)

• \(\theta\) = Scattering angle

• \(\theta_{E}\) = Characteristic inelastic scattering angle (~= E/2E₀) where E₀ is the primary beam energy

• \(a_{0}^{}\) = Bohr radius (0.529 Å)

• \(\nu\) = Electron velocity

• \(m_{0}\) = Electron rest mass

In this scenario

• Cross-section decreases with higher energy loss and accelerating voltage

• Angular distribution of cross-section follows Lorentzian distribution (approx.)

• Since \(\theta_{E}\) increases with energy loss, angular distribution broadens with \(E\)

The quantity \(df/dE\) is known as the generalized oscillator strength (GOS). It is through this term that the atom specific physics enters into the cross-section by means of a transition matrix of the form.

\(\left \langle \Psi _{f}\left | exp(iq.r) \right | \Psi _{i}\right \rangle\)

where  

• \(\Psi _{i}\) = Initial (core) electron state

• \(\Psi _{f}\) = Final (ionized) electron state

• \(q\) = Momentum transfer

In practice, there are two approaches you can take to determine the partial cross-section \(\sigma (\beta ,\Delta )\). You can evaluate values for GOS (\(q,E\)) in analytical form using hydrogenic approximations. This is incorporated into the SIGMAK and SIGMAL programs by Egerton; however, you can only compute K­- and L­-edge cross-­sections with these routines. Alternatively, you can numerically compute these values utilizing more sophisticated models of the atoms such as Hartree ­Slater atomic wave ­functions. Both these approaches are available in the DigitalMicrograph EELS analysis software. Keep in mind these approaches assume isolated, spherical atoms. The effects of bonding and crystallinity are not incorporated in these models.

Alternatively, you can measure edge intensities from known standard samples when you use a fixed set of experimental conditions and \(\sigma (\Delta ,\beta )\) that is derived from them. Caution, such measurements can be difficult and each reference covers only a limited range of \(\Delta\) and \(\beta\).

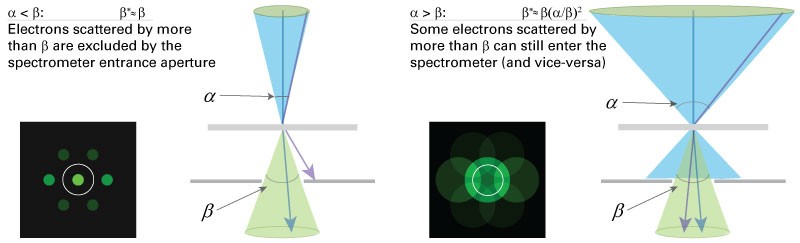
Effective collection angle \(\beta\)*

Knowledge of the effective collection angle \(\beta\)* is essential for accurate determination of the partial cross-section \(\sigma (\beta ^{*},\Delta )\). In the majority of cases in the conventional TEM you define the effective collection angle by the actual collection angle \(\beta ^{*}\cong \beta\). However, a convergence angle a of similar or greater magnitude to the collection angle will alter the partial cross-section. If this occurs, you should evaluate the effective partial cross-section \(\sigma (\alpha ,\beta,\Delta)\). If both angles are entered in the DigitalMicrograph EELS analysis software, the correct cross-section will be calculated. It is advisable to work in the regime where \(\beta\geq \alpha\) otherwise significant signal will be excluded from the detector.

Ideal collection angle \(\beta\)

When you increase \(\beta\), you will increase the total signal entering the spectrometer. However, beyond a certain angle (dependent on the edge energy) the background under the edge will start increasing faster than the edge signal. This crossover effect will lead to a maximum in the SNR for the edge.

As you optimize the collection angle \(\beta\) for EELS, it is important to keep in mind the below parameters.

To collect the maximum inelastic signal and minimum background, make the collection angle 2 – 3x the characteristic scattering angle \(\theta _{E}\) for the energy loss. The characteristic scattering angle \(\theta _{E}\) is the half width of the scattering distribution and is related is to the energy loss \(E\) and beam energy \(E_{0}\) via:

\(\theta _{E}\approx \frac{E}{2E_{0}}\)

e.g., Si K (1839 eV loss) at 200 kV, require 10 – 15 mrad collection angle

Error analysis

To ensure you attain the most robust results possible, it is important to pay close attention to the errors that may occur during analysis. Common errors include:

• Systematic errors

  • Uncertainty in the background model

  • Redistribution of signal from plural scattering; e.g., thicker regions when \(t/\lambda > 0.3\)

  • Uncertainty in experimental parameters; e.g., collection or convergence angle

  • Computation of cross-section

    • 5 – 10% for K-edges

    • 10 – 20% for L-edges

    • Much worse for M-, N-, O-edges

• Statistical errors

  • Uncertainty in background fit (e.g., \(h\) parameter)

  • Noise in signal integral (shot noise  sqrt(recorded intensity) shot noise = \(N{_{E}}^{1/2}\) )

Model-based quantification with GMS 3

In DigitalMicrograph^® 3 software, the extraction of the edge signals is approached somewhat differently. Rather than treating the edges and the background as two separate entities, they are treated as a single function. The background is treated as a power-law while the edges present are modeled by the theoretical cross-sections. This allows overlapping edges to be handled automatically. The effect of plural scattering is handled not by deconvolution of the extracted signal but by forward convolution of the model cross-section prior to fitting the model to the data. This results in a much better fit to the data and reliable extraction of overlapping edges. The method was inspired by the work of Veerbeeck and Van Aert (Verbeeck, J.; Van Aert, S. Model based quantification of EELS spectra. Ultramicroscopy. 101(2 – 4):207 – 24; 2004).

Steps for Quantification in GMS 3

1. Identify edges to quantify.

   
   
   

2. Click the Show signal setup icon (1) on the Elemental Analysis floating window to show the fit models.

3. You can then dynamically configure the fitting range from the Spectrum window.

4. Use the Analysis setup button (2) to configure each individual edge.

5. Within the EELS Edge Setup window, configure the background model and the cross-section type.

6. Edge overlaps are automatically determined. However, you can configure the overlap for each edge (a).

7. Use Exclude ELNES (b) for edges with strong white lines or extensive fine structure. This is also recommended if the low-loss spectrum is unavailable for this data.

8. When the low-loss is available and was acquired with the DualEELS function, the Include plural scattering checkbox will automatically be checked (c). When checked, the plural scattering correction is enabled or disabled (when unchecked) for all of the edges in the spectrum. The effect of plural scattering can be seen as shifting intensity in the model to higher energies.

9. Select the Quant button on the Elemental Analysis window to analyze the current spectrum. For spectra that include the low-loss data, an estimate of the spectrum thickness and volume density of the element will be calculated and displayed with the results.

10. For Spectrum Images, the Map button on the Elemental Analysis window will apply the quantification procedure on a pixel-by-pixel basis generating quantitative maps of the sample.